6576. Дорога
В одной стране имеется n дорог, пронумерованных
от 1 до n. Инженер-строитель должен возвести сеть дорог
общего пользования, которая соединит все города, то есть должна существовать
возможность добраться из любого города в любой другой, возможно, через
промежуточные города. Его команда обследовала несколько маршрутов (дороги между парами
городов). Каждая дорога является двусторонней. Постройка дороги требует
определённых затрат: чем короче маршрут, тем дешевле строительство.
Инженер никогда заранее не
проектировал дорожную систему. Он просто выбирает понравившуюся дорогу и строит
её, пока все города не окажутся соединены.
Теперь инженер хочет
построить дорогу между городами p и q. Под давлением правительства, стремящегося
сократить расходы, он просит вас написать программу, которая определит, стоит
ли строить эту дорогу. Ваша программа должна вывести “YES”, если после строительства
дорога (p, q) войдёт в минимальную
дорожную систему, соединяющую все города. В противном случае следует вывести “NO”.
Вход.
Первая строка содержит количество тестов t (t ≤ 10).
Каждый тест начинается
строкой из 4 целых чисел n, m, p и q. Здесь n (2 ≤ n ≤ 10000) – количество
городов, m (1 ≤ m ≤ 20000) – число дорог, а p и q (1 ≤ p, q ≤ n) задают города, между которыми
инженер собирается построить дорогу.
Далее следуют m строк, каждая из которых
содержит три числа u, v и w (1≤ u, v ≤ n, 1 ≤ w ≤ 4⋅105), описывающие существующую
двустороннюю дорогу длиной w между городами u и v. Длины всех дорог различны.
Между любой парой городов может существовать не более одной дороги.
Гарантируется, что граф связен, то есть между любой парой городов существует
путь. Все числа целые.
Выход. Для каждого теста выведите “YES”, если
дорога (p, q) будет входить в минимальную дорожную систему.
В противном случае выведите “NO”.
|
Пример входа |
Пример выхода |
|
3 2 1 1 2 1 2 4 3 3 2 3 1 2 1 1 3 2 2 3 3 4 5 3 4 1 2 1 1 3 3 3 4 2 1 4 4 4 2 5 |
YES NO YES |
РЕШЕНИЕ
графы – алгоритм Крускала
Анализ алгоритма
Запустим алгоритм Крускала
на исходном графе. В множество s добавим ребра, которые
входят в минимальное остовное дерево. Далее проверим, принадлежит ли заданное
ребро (p, q) этому остову. Для этого
необходимо проверить, содержится ли пара (p, q) или (q, p)
во множестве s.
Пример
Графы,
приведённые в примерах, имеют следующий вид:
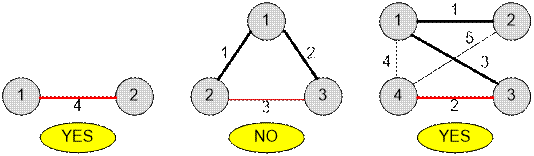
Реализация алгоритма
Объявим структуру ребра графа, содержащую
пару вершин и вес ребра. Объявим массив ребер e.
struct Edge
{
int u, v, dist;
};
vector<Edge> e;
Объявим
массив parent, используемый для реализации структуры
непересекающихся множеств.
vector<int> parent;
Функция Repr
находит представителя множества, к которому принадлежит вершина n.
int Repr(int n)
{
while(n != parent[n]) n = parent[n];
return n;
}
Функция Union объединяет
множества, содержащие элементы x и y.
int Union(int x, int y)
{
x = Repr(x); y = Repr(y);
if (x == y) return 0;
parent[y] = x;
return 1;
}
Функция lt служит
компаратором для сортировки ребер.
int lt(Edge a, Edge b)
{
return (a.dist < b.dist);
}
Основная
часть программы. Обрабатываем несколько тестов.
scanf("%d", &tests);
while (tests--)
{
Читаем
входные данные. Инициализируем массив parent.
scanf("%d %d %d %d", &n, &m, &p,
&q);
parent.resize(n + 1);
for (i = 1; i
<= n; i++) parent[i] = i;
Читаем
ребра графа.
e.resize(m);
for (i = 0; i < m; i++)
scanf("%d %d %d", &e[i].u, &e[i].v, &e[i].dist);
Сортируем
ребра графа по возрастанию их весов.
sort(e.begin(), e.end(), lt);
При
обработке каждого теста обнуляем переменную flag. Она принимает значение 1 или 0 в
зависимости от того, принадлежит ли ребро (p, q) минимальному остовному дереву.
flag = 0;
Запускаем
алгоритм Крускала для построения минимального остова. Если ребро (e[i].u, e[i].v) включается в минимальный остов,
проверяем, совпадает ли оно с ребром (p, q).
for (i = 0; i < m; i++)
if (Union(e[i].u, e[i].v))
Необходимо
проверить два условия: (e[i].u, e[i].v) = (p, q) и (e[i].u, e[i].v) = (q, p).
if ((e[i].u == p
&& e[i].v == q) ||
(e[i].u == q && e[i].v == p))
{
Если ребро
(e[i].u,
e[i].v) совпадает с (p, q) или (q, p), устанавливаем flag = 1 и выходим из цикла.
flag = 1;
break;
}
В зависимости от значения переменной flag выводим ответ.
if (flag)
puts("YES");
else
puts("NO");
}
Реализация алгоритма – set
Объявим структуру ребра графа, содержащую
пару вершин и вес ребра. Объявим массив ребер e.
struct Edge
{
int u, v, dist;
};
vector<Edge> e;
Объявим
массив parent, используемый для реализации структуры
непересекающихся множеств.
vector<int> parent;
Во
множестве s будем хранить рёбра, входящие в минимальное остовное дерево.
set<pair<int, int> > s;
Функция Repr
находит представителя множества, к которому принадлежит вершина n.
int Repr(int n)
{
while(n != parent[n]) n = parent[n];
return n;
}
Функция Union объединяет
множества, содержащие элементы x и y.
int Union(int x, int y)
{
x = Repr(x); y = Repr(y);
if (x == y) return 0;
parent[y] = x;
return 1;
}
Функция lt служит
компаратором для сортировки ребер.
int lt(Edge a, Edge b)
{
return (a.dist < b.dist);
}
Основная
часть программы. Обрабатываем несколько тестов.
scanf("%d", &tests);
while (tests--)
{
Читаем
входные данные. Инициализируем массив parent.
scanf("%d %d %d %d", &n, &m, &p,
&q);
parent.resize(n + 1);
for (i = 1; i
<= n; i++) parent[i] = i;
Читаем
ребра графа.
e.resize(m);
for (i = 0; i < m; i++)
scanf("%d %d %d", &e[i].u, &e[i].v, &e[i].dist);
Сортируем
ребра графа по возрастанию их весов.
sort(e.begin(), e.end(), lt);
При
обработке каждого теста очищаем множество s.
s.clear();
Запускаем
алгоритм Крускала для построения минимального остовного дерева. Если ребро (e[i].u, e[i].v) включается в остов, добавляем его во множество s.
for (i = 0; i < m; i++)
if (Union(e[i].u, e[i].v))
s.insert(make_pair(e[i].u, e[i].v));
После завершения алгоритма проверяем, принадлежит ли заданное ребро (p, q) минимальному остову. Для этого нужно
выяснить, содержится ли пара (p, q) или (q, p) во множестве s.
if ((s.find(make_pair(p, q)) != s.end()) ||
(s.find(make_pair(q,
p)) != s.end()))
puts("YES");
else
puts("NO");
}
Java реализация
import java.util.*;
class Edge
{
int u, v, dist;
Edge (int u, int v, int dist)
{
this.u = u;
this.v = v;
this.dist = dist;
}
};
class Pair
{
int u, v;
Pair (int u, int v)
{
this.u = u;
this.v = v;
}
};
public class Main
{
static int mas[];
static int size[];
static int Repr(int n)
{
if (n == mas[n]) return n;
return mas[n] = Repr(mas[n]);
}
static int Union(int x, int y)
{
x = Repr(x); y = Repr(y);
if(x == y) return 0;
if (size[x] < size[y])
{
int temp = x; x = y; y = temp;
}
mas[y] = x;
size[x] += size[y];
return 1;
}
public static class MyFun implements Comparator<Edge>
{
public int compare(Edge a, Edge b)
{
return a.dist - b.dist;
}
}
public static class PairFun implements Comparator<Pair>
{
public int compare(Pair a, Pair b)
{
if (a.u == b.u) return a.v - b.v;
return a.u - b.u;
}
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int tests = con.nextInt();
while(tests-- > 0)
{
int n = con.nextInt();
int m = con.nextInt();
int p = con.nextInt();
int q = con.nextInt();
mas = new int[n+1];
size = new int[n+1];
for(int i = 1; i <= n; i++)
{
mas[i] = i;
size[i] = 1;
}
Vector<Edge> v = new Vector<Edge>();
for(int i = 0; i < m; i++)
{
int x = con.nextInt();
int y = con.nextInt();
int dist = con.nextInt();
v.add(new Edge(x,y,dist));
}
Collections.sort(v, new MyFun());
TreeSet<Pair> s = new
TreeSet<Pair>(new PairFun());
for(int i = 0; i < m; i++)
if (Union(v.get(i).u,v.get(i).v) == 1) s.add(new Pair(v.get(i).u,v.get(i).v));
if(s.contains(new Pair(p,q)) || s.contains(new Pair(q,p)))
System.out.println("YES");
else
System.out.println("NO");
}
con.close();
}
}